Hello World

Hello World

几何图元（geometric primitives）

geometric primitives（几何图元），如点类型，被定义在kernel（内核）中，使用几何图元之前要指定内核。此处先使用double内核，可以理解为使用double作为坐标的数值类型，内核将在后面介绍。

几何图元可以理解为CGAL所内置的数据类型，如点类型、线段类型等等

几何谓词（geometric predicates）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
#include <CGAL/Simple_cartesian.h>              //在笛卡尔坐标系下
typedef CGAL::Simple_cartesian<double> Kernel;  //使用double类型的kernel
typedef Kernel::Point_2 Point_2;                //二维点、二维线段
typedef Kernel::Segment_2 Segment_2;
int main(){
    Point_2 p(1,1), q(10,10), m(5, 9); //点
    Segment_2 s(p,q);		  //线段

    // 两点距离
    CGAL::squared_distance(p,q);

    //点到线段距离的平方
    CGAL::squared_distance(s,m);

    //计算中点
    CGAL::midpoint(p,q);

    //三点的方向
    switch (CGAL::orientation(p,q,m)){
      case CGAL::COLLINEAR: //共线
        std::cout << "are collinear\n";
        break;
      case CGAL::LEFT_TURN: //p->q, q->m时向左转
        std::cout << "make a left turn\n";
        break;
      case CGAL::RIGHT_TURN: //p->q, q->m时向右转
        std::cout << "make a right turn\n";
        break;
	}   
    return 0;
}

谓词相当于方法或者函数

内核（Kernel）

计算几何一大坑：精度问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <iostream>
#include <CGAL/Simple_cartesian.h>
typedef CGAL::Simple_cartesian<double> Kernel; //使用double作为坐标的类型
typedef Kernel::Point_2 Point_2; //定义一个double类型的二维点
int main()
{
	{
		Point_2 p(0, 0.3), q(1, 0.6), r(2, 0.9); //实例化三个点
		std::cout << (CGAL::collinear(p, q, r) ? "collinear\n" : "not collinear\n"); //三个点是否共线
	}
	{
		Point_2 p(0, 1.0 / 3.0), q(1, 2.0 / 3.0), r(2, 1);
		std::cout << (CGAL::collinear(p, q, r) ? "collinear\n" : "not collinear\n");
	}
	{
		Point_2 p(0, 0), q(1, 1), r(2, 2);
		std::cout << (CGAL::collinear(p, q, r) ? "collinear\n" : "not collinear\n");
	}
	return 0;
}

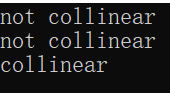
代码中的三个例子，手算的话，都应该是共线，但输出的结果是这样的：

image-20220714152452069

这是由于使用double所导致的（在计算的途中，由于精度的问题，可能会得到意想不到的结果）。如果要保证精度，可以使用内核Exact_predicates_exact_constructions_kernel。

精确谓词、精确构造的内核（Exact_predicates_exact_constructions_kernel）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
#include <CGAL/Exact_predicates_exact_constructions_kernel.h> 
#include <sstream>
typedef CGAL::Exact_predicates_exact_constructions_kernel Kernel; //精确谓词、精确构造的内核
typedef Kernel::Point_2 Point_2;
int main()
{
  Point_2 p(0, 0.3), q, r(2, 0.9);
  {
    q  = Point_2(1, 0.6);
    std::cout << (CGAL::collinear(p,q,r) ? "collinear\n" : "not collinear\n");
  }
  {
    std::istringstream input("0 0.3   1 0.6   2 0.9");
    input >> p >> q >> r;
    std::cout << (CGAL::collinear(p,q,r) ? "collinear\n" : "not collinear\n");
  }
  {
    q = CGAL::midpoint(p,r);
    std::cout << (CGAL::collinear(p,q,r) ? "collinear\n" : "not collinear\n");
  }
  return 0;
}

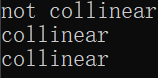
计算上述三个例子，不同的是kernel使用Exact_predicates_exact_constructions_kernel，结果如下：

image-20220714153223900

是不是很奇怪，第一个例子还是出错了。

分析：

  1. 第一个代码块中，这三个点仍然不是共线的。是因为它用文本传入的坐标，传入后变成了浮点数，转换成了任意精度的有理数时，它们仅表示浮点数，而可能不会精确的表示原来数值。
  2. 第二个代码块中。是从文件中读取数字，然后直接从字符串构造任意精度的有理数，以便它们能够精确的表示原来的数值。
  3. 在第三块中，中点是通过计算得出的，正如内核定义的那样，使用的是精确谓词，精确构造出来的，所以计算所得的精度是可以靠得住的（这便是第二种内核，精确构造、精确谓词的意思）

在许多情况中，就浮点数而言，它们是“精确的”，即它们是由某些应用程序计算或从传感器中获得的，是全精度的浮点数。它们不是文本0.1或动态计算”1.0/10.0”所得的（如果是这种方式得到的结果，可能不是精确的）。

精确谓词，但不精确构造的内核（Exact_predicates_inexact_constructions_kernel）

凸包算法仅仅比较坐标的数值和进行方向测试，故在凸包算法中（计算一个点集的凸包），输出的结果即是点集的子集，是原来的坐标值，而并不会重新构造出新的点。此类应用场景，即可使用精确谓词，但不精确构造的内核Exact_predicates_inexact_constructions_kernel。

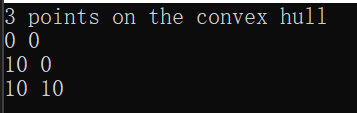
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/convex_hull_2.h>
typedef CGAL::Exact_predicates_inexact_constructions_kernel K; //精确谓词，但不精确构造的内核
typedef K::Point_2 Point_2;
int main()
{
	// 5个点
	Point_2 points[5] = { Point_2(0,0), Point_2(10,0), Point_2(10,10), Point_2(6,5), Point_2(4,1) };
	Point_2 result[5];
	// 计算2D凸包
	///参数：输入的起点、终点指针、凸包结果的指针数组
	///返回值：The function returns the pointer into the result array just behind the last convex hull point written,
	///so the pointer difference tells us how many points are on the convex hull.
	Point_2 *ptr = CGAL::convex_hull_2(points, points + 5, result);

	//凸包的个数=返回值-结果数组
	std::cout << ptr - result << " points on the convex hull:" << std::endl;

	for(int i = 0; i < ptr - result; i++)
	{
		std::cout << result[i] << std::endl;
	}

	return 0;
}

image-20220714154312112

说到2D凸包算法，这里展示另一种写法，使用vector存点集，在vector中计算凸包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/convex_hull_2.h>
#include <vector>

typedef CGAL::Exact_predicates_inexact_constructions_kernel K; //精确谓词，但不精确构造的内核
typedef K::Point_2 Point_2;
typedef std::vector<Point_2> Points;

int main()
{
	Points points, result;
	points.push_back(Point_2(0, 0));
	points.push_back(Point_2(10, 0));
	points.push_back(Point_2(10, 10));
	points.push_back(Point_2(6, 5));
	points.push_back(Point_2(4, 1));

	//2D凸包
	///第一二个参数：两个迭代器，表示输入的点集
	///第三个参数：计算结果所插入的位置
	CGAL::convex_hull_2(points.begin(), points.end(), std::back_inserter(result));

	std::cout << result.size() << " points on the convex hull" << std::endl;

	for(int i = 0, size = result.size(); i < size; ++i)
	{
		std::cout << result.at(i) << std::endl;
	}

	return 0;
}
1
2
3
4
5
6
7
std::back_inserter (Container& x);

x:Container in which new elements will 
be inserted at the end.

return：A back_insert_iterator that inserts 
elements at the end of container x

image-20220714155228911

特征类（Traits）

convex_hull_2()函数有两种版本

1.一种即是上面所提到的，使用两个迭代器来规定输入点的范围，并使用一个输出迭代器来将凸包结果写入到结果容器中

1
2
3
4
5
template <class ForwardIterator, class OutputIterator>
inline
OutputIterator 
convex_hull_2(ForwardIterator first, ForwardIterator last, 
              OutputIterator result)

2.第二个版本具有两个附加参数，一个是模板参数Traits和此此类型的参数ch_traits

1
2
3
4
5
template <class InputIterator, class OutputIterator, class Traits>
inline
OutputIterator
convex_hull_2(InputIterator first, InputIterator last,
              OutputIterator  result, const Traits& ch_traits)

第二个版本即是CGAL泛型编程的体现，Traits中定义了用户所使用类型的一些特征，让convex_hull_2()函数支持任意点类型，也可支持多种凸包算法。

「举例」以经典的凸包算法Graham/Andrew Scan为例，该算法先从左到右对点进行排序，然后从排序结果中逐个拿点构造凸包

（1）Traits类型

因此，若要完成凸包计算，必须要知道三个内容：点的类型、这个点类型的排序方式、三点的方向计算。而为了避免参数太多、太长，则将这些参数都定义在一个特征类中，即Traits类型中（CGAL每个Kernel中都有定义好的Traits类型）

（2）验证上面的说法

convex_hull_2()函数中用到了一个核心函数ch_graham_andrew()，具体定义如下：

1
2
3
4
5
template <class InputIterator, class OutputIterator, class Point_2, class Less_xy_2, class Left_turn_2, class Equal_2>
OutputIterator
ch_graham_andrew( InputIterator  first,
                  InputIterator  beyond,
                  OutputIterator result);

可以看到，如果要完成convex_hull_2()，必须要提供以下嵌套类型：

  • Traits::Point_2：自定义类型
  • Traits::Less_xy_2：点排序
  • Traits::Left_turn_2：方向测试
  • Traits::Equal_2：相等判断

而对于CGAL的每个模型，都有定义好的Traits。我们举个例子，来实现convex_hull_2()算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <iostream>
#include <iterator>
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h> 
#include <CGAL/Projection_traits_yz_3.h> 
#include <CGAL/convex_hull_2.h>

typedef CGAL::Exact_predicates_inexact_constructions_kernel K3; //精确谓词、不精确构造的Kernel
typedef CGAL::Projection_traits_yz_3<K3> K; //将3D投影到yz面的Traits
typedef K::Point_2 Point_2; //二维点

int main()
{
  std::istream_iterator< Point_2 >  input_begin( std::cin );
  std::istream_iterator< Point_2 >  input_end;
  std::ostream_iterator< Point_2 >  output( std::cout, "\n" );
  CGAL::convex_hull_2( input_begin, input_end, output, K() );
  return 0;
}